Феномен аннигиляции и рождения электрон-позитронных пар оказался, на первый взгляд, камнем преткновения для принципа автономных превращений энергии [1]. Этот принцип утверждает, что квантовый пульсатор, т.е. элементарный “кирпичик” вещества, может приобрести кинетическую энергию или энергию связи лишь за счёт убыли собственной энергии, т.е. за счёт уменьшения частоты квантовых пульсаций. Другими словами, у электрона (и позитрона) могут происходить лишь внутренние перераспределения энергии трёх названных форм, но электрон не может ни приобрести дополнительной энергии откуда-то извне, ни отдать часть энергии куда-то вовне. Тем более, электрон и позитрон не могут исчезнуть с полным превращением в g -излучение – и наоборот, g -квант не может превратиться в электрон и позитрон, которых до этого не существовало.

Казалось бы, огромное количество экспериментов, в которых исследовались аннигиляция и рождение электрон-позитронных пар, должно привести нас к выводу о том, что в данной области принцип автономных превращений энергии не работает. Однако, наш анализ этих экспериментов обнаруживает, что их результаты допускают интерпретацию, согласно которой, в отличие от традиционных представлений об аннигиляции, электрон и позитрон не исчезают полностью, а образуют “предельно связанную пару” с энергией связи 511 кэВ – которая в точности равна энергии одного кванта характеристического аннигиляционного излучения. Соответственно, предельно связанная пара может диссоциировать, порождая иллюзию рождения пары электрон-позитрон.

В статье [1] был дан ответ на вопрос о том, какая максимальная часть собственной энергии покоя квантового пульсатора может превратиться в его кинетическую энергию (“покой”, “движение”, “кинетическую энергию” следует понимать в локально-абсолютном смысле: скорость движения – это локально-абсолютная скорость [2]). Но вопрос о том, какая максимальная часть собственной энергии покоя может превратиться в энергию связи, не был рассмотрен.

Связанную пару электрон-позитрон, которая имеет максимально возможную энергию связи, мы называем предельно связанной парой. Следует иметь в виду, что предельно связанные электрон и позитрон, фактически, не являются электроном и позитроном как таковыми. Собственные частоты их пульсаций уменьшены вдвое по сравнению с частотой пульсаций свободного покоящегося электрона, т.е. по сравнению с электронной частотой, поэтому ни один из партнёров предельно связанной пары не обладает электрическим зарядом, и, соответственно, магнитный момент этой пары должен быть равен нулю. Масса же предельно связанной пары, как можно видеть, равна массе свободного электрона; при этом относительный дефект масс рекордно велик. Используя формулы статьи [1], можно оценить расстояние, которое должно разделять центры предельно связанных электрона и позитрона: оно составляет ~ 2.8× 10^-15 м, что поразительным образом соответствует характерным размерам атомных ядер. Следует подчеркнуть, что предельно связанные электрон и позитрон не имеют ничего общего с позитронием, который, как полагают, представляет собой образование из полноценных электрона и позитрона, вращающихся вокруг общего центра масс. Позитроний нестабилен и исчезает в результате аннигиляции. Напротив, предельно связанная пара весьма стабильна; её стабильность, как мы полагаем, должна быть заведомо не хуже стабильности устойчивых атомов – поскольку партнёры предельно связанной пары удерживаются по тому же принципу, что и атомарные электроны около ядра [1].

“Излучение” при образовании предельно связанных пар должно иметь одну принципиальную особенность. По традиционным представлениям, электрон и позитрон при аннигиляции исчезают полностью, так что при этом должна “излучиться” энергия, соответствующая двум массам свободного электрона. С учётом закона сохранения импульса, наиболее вероятно “излучение” этой энергии двумя квантами по 511 кэВ – в противоположных направлениях. В рамках же нашей модели, при образовании предельно связанной пары электрон и позитрон теряют по половине своих масс, и в результате должна “излучиться” энергия, соответствующая одной массе свободного электрона. Причём, если предельно связанная пара образуется не в результате ступенчатого процесса, а скачкообразно, то энергия в 511 кэВ должна “излучиться” одним квантом. Это не противоречило бы закону сохранения импульса: даже если фотоны переносили бы импульс (а мы полагаем, что это не так [3]), то необходимый импульс отдачи могла бы принять на себя образовавшаяся пара. Таким образом, как традиционные представления, так и наша модель дают одинаковые предсказания для энергии аннигиляционных квантов – 511 кэВ. Эта энергия соответствует результатам прецизионных измерений длины волны аннигиляционного излучения – например, с помощью длиннофокусного спектрометра с вогнутым кристаллом [4,5], причём эта длина волны обеспечивает одну из важнейших калибровок в g -спектроскопии [6]. Вопрос лишь в том, один или два кванта по 511 кэВ “излучаются” при одном акте аннигиляции пары электрон-позитрон.

Считается, что этот вопрос давно и бесповоротно решён на опыте в пользу двух “разлетающихся” квантов по 511 кэВ. Давайте же посмотрим, на чём основано такое решение.

Пионерской считается статья Клемперера [7], которая труднодоступна. К счастью, в статье [8] недвусмысленно сказано, что Клемперер “детектировал совпадающие импульсы с двух счётчиков Гейгера, расположенных вплотную к источнику излучения аннигиляции, так что телесный угол, в котором собирал излучение каждый из этих счётчиков, составлял почти 2p ” (перевод наш). Конечно, не могло быть гарантий, что совпадения не порождались квантами от независимых актов аннигиляции, случайно совпадавших во времени. Поэтому в дальнейшем исследователи старались улучшить угловое разрешение установки.

Известна, например, заметка советских авторов [9], но она настолько лаконична, что невозможно судить об обоснованности их вывода насчёт “испускания двух квантов в прямопротивоположных направлениях”.

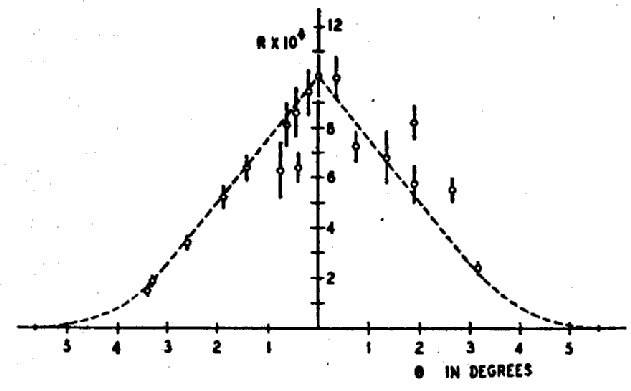
Напротив, работа [8] достаточно обстоятельна. В качестве источника излучения аннигиляции там использовались активированные кусочки фольги Cu⁶⁴, спрессованные в маленькую “пилюлю”, которая покрывалась тонким слоем свинца, не пропускавшим наружу позитроны. Такая “пилюля” излучала, практически, в полный телесный угол. Два счётчика располагались на равных расстояниях по разные стороны от неё – с возможностью механической отстройки от “правильной” геометрии, при которой источник и оба счётчика находятся на одной прямой. Полученная скорость счёта совпадений, как функция угла отстройки от “правильной” геометрии, вызывает недоумение; мы воспроизводим диаграмму из [8].

Сразу бросается в глаза, что уменьшение скорости счёта совпадений при увеличении угла отстройки выглядит неубедительно: подавляющее большинство точек даёт примерно одну и ту же скорость счёта. Более того: четыре точки, которые дают уменьшенную скорость счёта совпадений при больших углах отстройки, имеют, по сравнению с остальными точками, существенно меньшие доверительные интервалы. А поскольку эти интервалы “вычислены на основе количества отсчётов, взятых в обработку для каждой точки” (перевод наш), то неизбежен вывод: четыре названные точки были получены в иных условиях опыта, чем остальные, а именно – при существенно увеличенных выборках. Нетрудно видеть, к чему это должно было привести. У случайной последовательности импульсов интервалы между двумя соседними импульсами имеют гауссовское распределение вероятностей с центром, соответствующим средней частоте появления импульсов. Увеличение выборки не сдвигает центр этого распределения, но изменяет его форму, увеличивая вероятности для значений интервалов в области центра распределения. Соответственно, при этом уменьшаются вероятности для значений интервалов на “крыльях” распределения – в том числе и для коротких интервалов, меньших временного разрешения схемы совпадений. В итоге, увеличение выборки в рассматриваемом эксперименте должно было привести к уменьшению вероятности срабатывания схемы совпадений – и, значит, именно к уменьшению средней скорости счёта совпадений.

С появлением более совершенных счётчиков, в частности, сцинтилляционных, эксперименты по уточнению “угловых корреляций” аннигиляционного излучения были продолжены. Идеология регистрации совпадений осталась прежней; в качестве же важного новшества, из всего излучения аннигиляции стали вырезать лишь два узких противоположно направленных пучка – как правило, с помощью свинцовых коллиматоров. На каждый из этих пучков “сажали” счётчик, и, сдвигая один из счётчиков поперёк пучка, исследовали “угловые корреляции”. По этой методике работали с излучением аннигиляции из различных образцов: непосредственно из активированных опилок Cu⁶⁴ [10], из кварца [11], из металлических фольг [12], из различных, в том числе диэлектрических, твёрдых веществ [13] и даже из сжатых газов [14]. При этом типичная зависимость скорости счёта совпадений от угла, определяемого поперечным сдвигом подвижного счётчика, представляла собой нечто похожее на гауссоиду. Её максимум соответствовал “правильной” геометрии, а ширина удивительно хорошо коррелировала с отношением диаметра пучка на щели счётчика к расстоянию от счётчика до источника. Подобные особенности, казалось бы, должны были с очевидностью указывать на происхождение полученных зависимостей. Ведь ясно, что скорость счёта каждого из счётчиков максимальна тогда, когда он “сидит” на центре своего пучка. Если сдвигать один из счётчиков, выводя сцинтиллятор из пучка, то скорость счёта этого счётчика будет, разумеется, уменьшаться – а, значит, будет уменьшаться и скорость счёта совпадений. Поэтому полученные “угловые корреляции”, вплоть до нескольких миллирадиан, характеризуют отнюдь не разброс почти противоположных направлений “разлёта” продуктов двухфотонной аннигиляции – они, как можно видеть, имеют чисто аппаратурный характер, отражая результаты угловой разъюстировки экспериментальной сборки.

Например, можно было получить последовательности импульсов с обоих счётчиков в режиме свободного счёта (не в режиме совпадений) и, совместив эти две последовательности, построить гауссовское распределение вероятностей для интервалов между соседними импульсами. Это распределение сразу же дало бы вероятность случайного попадания двух импульсов в пределы временного разрешения схемы совпадений – на основе чего можно было оценить среднюю скорость счёта случайных совпадений. Если же, как полагают, регистрировавшиеся совпадения были скоррелированными, то скорость их счёта должна была превышать скорость счёта случайных совпадений на несколько порядков – и она, по условиям опытов, была бы сравнима со скоростью свободного счёта. В действительности же, например, в эксперименте [8], скорость счёта совпадений была меньше скорости свободного счёта на три порядка. Весьма похоже, что срабатывания схемы совпадений вызывались g -квантами, “излучёнными” всё-таки в независимых друг от друга актах аннигиляции.

В качестве ещё одной подстраховки, следовало бы “посадить” счётчики на два пучка, выходящих из области аннигиляции в направлениях, существенно отличающихся от противоположных. Эта проверка поставила бы крест на традиционной модели двухфотонной аннигиляции, так как схема совпадений исправно работала бы и при такой “неправильной” геометрии. Мы говорим об этом с уверенностью, поскольку подобный эксперимент, к счастью, был проделан.

Речь идёт об эксперименте [15], где, как полагают, исследовалась аннигиляция позитронов “на лету”. Сколлимированный пучок позитронов направлялся на полимерную плёнку, где происходила аннигиляция позитронов с атомарными электронами. Целью эксперимента была проверка второго постулата специальной теории относительности – о независимости скорости света от скорости движения источника – через сравнение, с помощью схемы совпадений, пролётных времён g -квантов, “излучаемых” почти вперёд и почти назад при двухфотонной аннигиляции “на лету”. По логике экспериментатора, роль источника в данном случае играет центр масс пары электрон-позитрон, который движется со скоростью в половину скорости света – поскольку позитроны в пучке движутся практически со скоростью света. При этом пара квантов аннигиляции, якобы, должна разлетаться не вполне в противоположных направлениях: с учётом энергии позитронов, детекторы были установлены в направлениях под углами 20° и 135° к падающему пучку. В результате никакой разницы для пролётных времён g -квантов, “летящих” в этих направлениях, обнаружено не было. Но следует обратить внимание на то, что энергетические коридоры обоих каналов схемы регистрации составляли “от 0.511 до 0.65 МэВ”. При движении источника со скоростью в половину скорости света, кванты аннигиляции не попадали бы в заданный энергетический коридор из-за линейного эффекта Допплера. Следовательно, детекторы регистрировали кванты аннигиляции, “излучаемые” практически неподвижными источниками. Действительно, хорошо известно, что спектр аннигиляционного излучения – даже из образцов, бомбардируемых быстрыми позитронами – практически не имеет допплеровского уширения. Это объясняют тем, что быстрые позитроны, при влёте в конденсированную среду, эффективно тормозятся до тепловых скоростей, и лишь затем аннигилируют. Таким образом, результат эксперимента [15] мало пригоден для подтверждения второго постулата специальной теории относительности. Но зато этот результат говорит о другом: схема совпадений исправно работает, когда детекторы регистрируют кванты аннигиляции, “излучённые” покоящимся источником отнюдь не в противоположных направлениях. Этот факт полностью обесценивает результаты экспериментов с противоположно направленными пучками излучения аннигиляции – которые, стало быть, ничуть не доказывают справедливость традиционной двухфотонной модели.

Традиционный теоретический сценарий рождения пар таков: g -квант с достаточно большой энергией исчезает вблизи достаточно тяжёлого ядра, порождая электрон-позитронную пару “в кулоновском поле ядра”. Этот сценарий не представляет для нас интереса, поскольку на практике он неотличим от другого, на наш взгляд, более правдоподобного: g -квант возбуждает ядро, которое затем испытывает сразу два бета-распада – с выстреливанием электрона и позитрона.

Теперь обратим внимание на то, что при образовании предельно связанной пары “излучается” один квант в 511 кэВ. Поскольку эта энергия как раз равна энергии связи у предельно связанной пары, то квант, “излучённый” при образовании одной такой пары, способен эффективно разрушить другую. При достаточно сильном инициирующем воздействии, цепочки многократных диссоциаций-рекомбинаций предельно связанных пар могут производить впечатление лавинообразного “рождения” электронов и позитронов. Весьма похоже, что в этом и заключается разгадка электрон-фотонной компоненты каскадных ливней [16], порождаемых частицами космических лучей с высокой энергией. Такая частица, на наш взгляд, не только разбивает предельно связанные пары на своём пути, она ещё может выбивать из ядер вторичные частицы, которые, в свою очередь, тоже могут разбивать предельно связанные пары. Фотографии электрон-позитронных ливней, возникающих при прохождении космической частицы сквозь свинцовые пластинки в камере Вильсона, приведены, например, в [17,16]. Традиционная интерпретация феномена такова: все эти электроны и позитроны, оставляющие треки, рождаются за счёт убыли кинетической энергии инициирующей частицы. В рамках этого подхода можно сделать нижнюю оценку стартовой энергии инициирующей частицы – хотя бы по числу треков в ливне. Хорошо известно, что подобные оценки, особенно для случаев сильных ливней, дают значения кинетических энергий, которые на многие порядки превышают энергию покоя инициирующей частицы. Такое положение дел противоречило бы принципу автономных превращений энергии, согласно которому, кинетическая энергия частицы появляется за счёт убыли её собственной энергии, и даже в релятивистском случае кинетическая энергия не может превышать одной трети собственной энергии покоя [1]. Поэтому мы полагаем, что тезис о рождении ливневых частиц за счёт убыли кинетической энергии инициирующей частицы является некорректным. Если релятивистский протон из космических лучей терял бы кинетическую энергию только на разрушение предельно связанных пар, то на всём своём пути он смог бы разрушить ~ 600 таких пар. Число треков сильного ливня гораздо больше, и, на наш взгляд, большинство этих треков оставляют электроны и позитроны вторичные, третичные, и т.д., “возникающие” и “пропадающие” в цепочках диссоциаций-рекомбинаций предельно связанных пар – что происходит без потерь энергии инициирующей частицы.

Казалось бы, наша версия противоречит тому, что регистрируемое направление развития ливня совпадает с направлением полёта инициирующей частицы – ведь, при разрушениях предельно связанных пар резонансными g -квантами, направления разлётов электронов и позитронов должны быть равновероятны. Но в отсутствии здесь противоречия нас убеждает одна тонкость, заметная на типичных фотографиях ливней. Дело в том, что зачастую подавляющее большинство треков ливневых частиц, вылетающих из свинцовой пластинки, имеет общую начальную точку, которая расположена на задней поверхности пластинки, совпадая с точкой выхода инициирующей частицы. Мы интерпретируем эту тонкость следующим образом. Электроны и позитроны, освобождаемые в толще свинцовой пластинки при разрушениях предельно связанных пар, действительно разлетаются во всевозможных направлениях, но в свинце их пробег ничтожен; лишь вблизи выхода из пластинки у освобождённых электронов и позитронов появляется возможность вылететь в переднюю (по ходу инициирующей частицы) полусферу: они-то и оставляют треки.

С учётом представленного выше анализа, основополагающие эксперименты по исследованию аннигиляционного излучения отнюдь не доказывают, что при одном акте аннигиляции электрон-позитронной пары “излучаются” два кванта по 511 кэВ в противоположных направлениях. Более того, предпочтительнее выглядит версия о “излучении” только одного кванта в 511 кэВ – при образовании предельно связанной пары.

Интересно, что этого полного превращения не происходит даже при взаимодействии электрона и позитрона, хотя они являются, по-видимому, единственной парой частица-античастица со “стопроцентным антагонизмом”. Действительно, мы полагаем, что противоположные электрические заряды порождаются противофазными квантовыми пульсациями на электронной частоте [18], причём электронная частота характеризует всю собственную энергию у покоящегося свободного электрона или позитрона. Напротив, у протона и антипротона электронная частота соответствует лишь ничтожной части их собственных энергий, и можно ожидать, что при их аннигиляции процентный выход излучения будет ещё меньшим, чем при аннигиляции электрон-позитронной пары. И это действительно так: даже среди физиков не очень широко известно о том, что, вопреки расхожим представлениям об аннигиляции вещества и антивещества, протон и антипротон превращаются не в излучение, а в несколько p -мезонов [19].

1. А.А.Гришаев. Автономные превращения энергии квантовых пульсаторов – фундамент закона сохранения энергии. – Доступна на данном сайте.
2. А.А.Гришаев. Эксперимент Майкельсона-Морли: детектирование локально-абсолютной скорости? – Доступна на данном сайте.
3. А.А.Гришаев. Масса, как мера собственной энергии квантовых осцилляторов. – Доступна на данном сайте.
4. J.W.M.DuMond, et al. Phys.Rev., 75, 8 (1949) 1226.
5. D.E.Muller, et al. Phys.Rev., 88, 4 (1952) 775.
6. М.Дейч, О.Кофед-Хансен. Гамма-излучение ядер. В кн.: Экспериментальная ядерная физика. Под ред. Э.Сегре. Т. 3. “Изд-во иностр. лит-ры”, М., 1961.
7. O.Klemperer. Proc.Camb.Phil.Soc., 30, (1934) 347.
8. R.Beringer, C.G.Montgomery. Phys.Rev., 61, March 1-15 (1942) 222.
9. А.И.Алиханьян и др. ДАН СССР, т. 1(10), N 7(84) (1936) 275.
10. S.DeBenedetti, et al. Phys.Rev., 77, 2 (1950) 205.
11. L.A.Page, et al. Phys.Rev., 98, 1 (1955) 206.
12. G.Lang, et al. Phys.Rev., 99, 2 (1955) 596.
13. L.A.Page, M.Heinberg. Phys.Rev., 102, 6 (1956) 1545.
14. M.Heinberg, L.Page. Phys.Rev., 107, 6 (1957) 1589.
15. D.Sadeh. Phys.Rev.Lett., 10, 7 (1963) 271.
16. Л.Яносси. Космические лучи. “Изд-во иностр. лит-ры”, М., 1949.
17. Д.Д.Странатан. “Частицы” в современной физике. “Гос. изд-во технико-теоретической лит-ры”, М.-Л., 1949.
18. А.А.Гришаев. Разноимённые электрические заряды, как противофазные квантовые пульсации. – Доступна на данном сайте.
19. К.Н.Мухин. Экспериментальная ядерная физика, Т.2. “Атомиздат”, М., 1974.