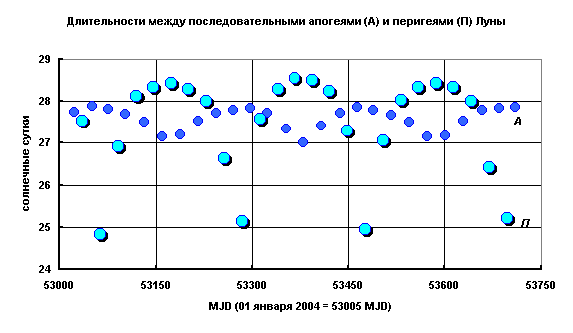
ПЕРИОДИЧЕСКОЕ ДВИЖЕНИЕ ПОЛЮСОВ ЗЕМЛИ: РЕАЛЬНОСТЬ ИЛИ ИЛЛЮЗИЯ?
А.А.Гришаев
Государственный эталон времени-частоты, ФГУП “ВНИИФТРИ”
141570 Московская обл., Менделеево
Введение.
Считается, что, при практически неизменной ориентации оси вращения Земли относительно “неподвижных звёзд”, фигура вращающейся Земли испытывает “покачивания” вокруг оси вращения. При этом точки пересечения оси вращения с поверхностью фигуры Земли перемещаются по этой поверхности. Согласно принятой терминологии, это явление называют периодическим движением полюсов Земли [1-3]. По результатам более чем столетних наблюдений считается, что размах “качаний” полюса по приполярной поверхности может достигать пары десятков метров. Это значительная величина для современных практических приложений, зависящих от качества координатно-временного обеспечения. Поэтому движение полюсов непременно принимается во внимание в современных навигации, астрометрии, геодезии, и т.д.
Начало истории вопроса связывают с построением Эйлером, в конце XVIII в., теории вращательного движения твёрдого тела с закреплённой точкой в отсутствие внешних сил. Помимо прецессии оси вращения, теория предсказывала также нутацию, т.е. покачивание, по отношению к оси вращения, фигуры вращающегося тела. В отличие от “вынужденной нутации” Земли, с периодом 18.6 лет, которую связывают с движением узлов орбиты Луны, “свободная нутация” Земли, по Эйлеру, обусловлена единственно эллипсоидальным сжатием её фигуры. Для периода свободной нутации Земли Эйлер получил величину примерно в 305 суток.
Спустя столетие, на основе астрономических наблюдений выявились периодические изменения широт наземных пунктов. Эти изменения широт имели две главных компоненты: с постоянным годичным и переменным чандлеровским (410-435 суток) периодами. Было найдено, что в пунктах с противоположными долготами изменения широт происходят в противофазе. Тогда и был сделан вывод о покачиваниях, вокруг оси вращения, фигуры вращающейся Земли. Происхождение годичной компоненты движения полюса связали с сезонными геофизическими процессами, а чандлеровскую компоненту посчитали проявлением эйлеровой свободной нутации.
Однако, этот подход с самого начала сталкивался с такими теоретическими трудностями – особенно в отношении чандлеровской компоненты – что сегодня его корректность не просто ставится под сомнение, а некоторыми авторами даже полностью отрицается [4]. Предлагаются, тоже не бесспорные, альтернативные объяснения “качаний” полюса – например, на основе гипотезы о вынужденных перемещениях внутреннего ядра Земли [4,5], или на основе сложной математической модели поступательно-вращательного движения Земли, которая “деформируема под действием центробежных сил инерции и гравитационного поля Луны” [6], причём в этой модели используются произвольно введённые динамические параметры. Но никто из авторов не усомнился в реальности периодического движения полюсов.
Между тем, следствием развиваемой нами модели тяготения является радикальный вывод: вышеназванные глобально скоррелированные изменения широт наземных пунктов обусловлены причинами, не связанными с движением полюсов. При этом объяснение чандлеровской компоненты оказывается невероятно простым.
Трудности традиционного подхода.
Происхождение годичной компоненты “качаний” полюса связывают, главным образом, с сезонными перемещениями масс Земли [2,3] – в частности, с формированием зимнего антициклона в Сибири и с нарастанием там снежного покрова. Однако динамика этих процессов варьируется от года к году и, конечно, не может обеспечить двух почти идеальных синусоид, по которым происходят годичные колебания координат полюса
xp и yp.Впрочем, главные трудности традиционного подхода связаны с чандлеровской компонентой. Прежде всего, чандлеровский период существенно больше эйлеровского. Ньюкомб связал этот факт с отличиями Земли от твёрдого тела – с её упругостью и деформируемостью – хотя, напомним, свободная нутация является решением задачи о вращении твёрдого тела. К тому же ясно, что свободная нутация упругой и деформируемой Земли непременно должна затухать – но чандлеровская компонента демонстрирует неплохую регулярность на более чем столетнем интервале наблюдений. Говорят о “механизме возбуждения” чандлеровских колебаний, но природа этого механизма до сих пор не установлена. Как ни парадоксален был вклад Ньюкомба, после него “теории вращения Земли стали строиться на основе модели внутреннего строения Земли, а наблюдаемые параметры вращения, в свою очередь, рассматриваться в качестве критериев для принятия соответствующей модели Земли” [7]. Как следствие, модели внутреннего строения Земли становились всё более экзотическими – поскольку, для подтягивания величины периода свободной нутации к чандлеровскому значению, приходилось “земную твердь” всё в большей степени считать “земной хлябью”.
Между тем, известны аргументы Ю.Н.Авсюка [4], вытекающие из связи между периодом нутации и динамическим сжатием Земли, равным (С
-А)/С, где С и А – моменты инерции Земли относительно полярной и экваториальной осей. Утверждение о том, что чандлеровский период является периодом свободной нутации, приводит к двум парадоксальным следствиям. Во-первых, динамическое сжатие должно составлять » 1/427, что отличается от величины » 1/305, определённой по скорости предварения равноденствия. “Допускать, что одна и та же характеристика реальной Земли имеет два различающихся на ~ 40% значения, нелогично, потому что это различие на несколько порядков превышает точность наблюдений” [4]. Во-вторых, полярный момент инерции Земли должен быть больше, чем у однородного шара того же радиуса. Тогда “необходимо принять, что плотность в Земле уменьшается с глубиной” [4] – что, конечно, противоречит данным о прохождении сейсмических волн в толще Земли.Поистине, “сказанного достаточно, чтобы отбросить подход к объяснению изменяемости широт как проявлению свободной нутации Земли” [4].
Изменяемость широт и вариации силы тяжести.
Поразительным фактом, проливающим свет на природу изменяемости широт, является соответствие вариаций широт вариациям силы тяжести.
Что касается короткопериодических вариаций, то суточные колебания широт были обнаружены раньше, чем приливные вариации силы тяжести. К.А.Куликов пишет: “Суточный член в изменениях широты был обнаружен в наблюдениях на Пулковской и на некоторых других обсерваториях. Впервые на короткопериодические изменения широты обратил внимание М.Нюрен в 1872 г. …Но тогда этот вопрос был совершенно новым и никому не приходила мысль, что эти колебания происходят с суточным периодом. Когда начались массовые наблюдения за изменяемостью широт с применением цепного метода, то выяснилось, что в среднем значения широт по вечерним группам систематически отличаются от широт, выведенных по группам утренним… Всем хорошо известны, но никем толком не изучены многолетние наблюдения А.С.Васильева… Основной вывод… заключается в том, что существуют суточные колебания в наблюдённых зенитных расстояниях с амплитудой 0² .16” [2]. Эта величина сравнима с амплитудой годично-чандлеровской волны! Но вывод о суточных колебаниях широт не вписывается в традиционные теории вращения Земли – чем, по-видимому, и объясняется игнорирование этого вывода научным сообществом.
Что же касается долгопериодических вариаций, то здесь в теорию плохо вписывались данные не широтных, а гравиметрических измерений. В литературе появился термин “неприливные вариации силы тяжести”. “К неприливным вариациям относятся все систематические расхождения, которые остаются после исключения из наблюдаемой вариации силы тяжести g(t) эффектов… приливного воздействия Луны и Солнца… Когда трудно установить явное соответствие хода неприливной вариации ходу какого-либо природного процесса, её относят к погрешности аппаратуры, к так называемому дрейфу нуля прибора. В этом случае сведения о ней обычно не публикуются” [5]. Но обнаружилось, например, что “дрейф нуля сейсмометра, установленного в Ленинграде, подобен дрейфу нуля гравиметра, установленного под Алма-Атой… Такое подобие показаний приборов разной конструкции не может быть объяснено ни аппаратурной погрешностью, ни локальными процессами… автор сделал заключение о наличии неприливной вариации, обусловленной каким-то глобальным процессом. Мы обратили внимание, что временной ход этой глобальной вариации коррелирует с лунными фазами” [5]. Был сделан вывод о “глобальной неприливной вариации с амплитудой порядка 30× 10-6 см/с2 и с цикличностью, соответствующей смене лунных фаз (синодическому месяцу)” [5]; о глобальных неприливных вариациях силы тяжести речь идёт также в [8-10]. Опубликован тезис об “удовлетворительных частотных эквивалентах изменений приливной силы изменениям широт”, и там же: “Чандлерова периодичность имеет эквивалент в вариациях приливной силы и не претендует на исключительность” [4].
Итак, два не вполне понятных феномена – изменяемость широт и вариации силы тяжести – в широком диапазоне частот коррелируют друг с другом. С учётом этой корреляции, логичным представляется поиск объяснения, которое работало бы для обоих названных феноменов. Мы предлагаем, на наш взгляд, подходящее объяснение. Вспомним, что “определяемая из астрономических наблюдений широта места есть угол между отвесной линией в данном месте и плоскостью экватора, которая задаётся положением оси вращения Земли” [1]. Изменения широт могут вызываться уклонениями местных отвесных линий по причинам, не связанным с движением полюсов – такие изменения широт называют неполярными. Теперь обратим внимание: согласно нашей модели тяготения, направления местных отвесных линий испытывают вращательные колебания, две главных компоненты которых имеют периоды в солнечные и в лунные сутки [11]. Спокойная поверхность воды ортогональна местной вертикали
, поэтому именно вращательные колебания местных вертикалей, на наш взгляд, порождают региональные вращающиеся приливные волны в Мировом океане [11]. Ясно, что вращательные колебания местных вертикалей должны вызывать соответствующие неполярные изменения широт. Мы постараемся показать, что те самые уклонения местных вертикалей, которые, на наш взгляд, являются истинными генераторами океанских приливов, ответственны и за те обнаруживаемые при астрономических наблюдениях изменения широт, которые посчитали следствием периодического движения полюсов.Иллюзия движения полюсов при астрономических наблюдениях.
“Солнечные” и “лунные” колебания широт.
Вращательные колебания направлений местных вертикалей, о которых идёт речь, обусловлены, на наш взгляд, некоторыми особенностями сообщения веществу Земли ускорений в системах Солнце-Земля и Земля-Луна. А именно: солнечно-суточная компонента этих колебаний порождается динамическим сдвигом, в сторону Солнца, центра тяготения Земли относительно центра геоида [11], а лунно-суточная компонента – неодинаковой эффективностью передачи ускорения, в сторону Луны, различным элементам объёма Земли [11].
Каждое из двух результирующих неполярных колебаний широты, как “солнечное”, так и “лунное”, для пунктов на средних широтах можно приближённо описать суммой быстрого суточного члена и медленной составляющей, зависящей от склонения соответствующего светила. Так, для пункта на “истинной” широте j , “солнечные” колебания широты должны иметь вид
D j C» (d/R)[sinj × sin(2p t/TC)+cosj × sind С], (1)
где
d» 1.6 м – динамический сдвиг, в сторону Солнца, центра тяготения Земли относительно центра геоида, R - средний радиус Земли, TC - солнечные сутки, d С - склонение Солнца, которое изменяется с периодом в один год. Аналогично, “лунные” колебания широты для того же пункта должны иметь видD j Л» (a/g)[sinj × sin(2p t/TЛ)+cosj × sin(2p t/TSIN)× sind Л], (2)
где
a - модуль ускорения Земли в системе Земля-Луна, g - модуль местного ускорения свободного падения, TЛ - лунные сутки, TSIN - синодический месяц, d Л - склонение Луны.Следует уточнить, что склонение Луны изменяется с периодом, близким к сидерическому месяцу
TSID, так что d Л» d 0× sin(2p t/TSID), где d 0 – амплитудное значение склонения Луны, максимальная величина которого достигает » 28о.5. Кроме того, поскольку апогейное и перигейное удаления Луны от Земли различаются на 13%, ускорение Земли в системе Земля-Луна испытывает апогей-перигейные вариации с размахом 26%. Таким образом, ускорение a в (2) также является периодической функцией: a=a0+0.13× a0× sin(2p t/TАП), где a0=3.3× 10-5 м/с2, TАП – период апогей-перигейного цикла. Для упрощения записей, мы не показываем постоянные сдвиги фаз у периодических функций.Величина “лунных” колебаний на порядок больше, чем “солнечных”, и мы постараемся показать, что обе главные компоненты “качания” полюса – чандлеровская и большая часть годичной – проистекают из “лунных” неполярных колебаний широты.
Простое объяснение происхождения чандлеровской компоненты.
Сопоставляя периоды характерных лунно-солнечных циклов, имеющих отношение к рассматриваемой задаче, мы обратили внимание на то, что разность частот у апогей-перигейного и синодического циклов представляет собой как раз частоту чандлеровских колебаний.
Таким образом, волну с чандлеровским периодом могло бы дать произведение апогей-перигейной и синодической волн, но в “лунных” колебаниях широты (2) такое произведение в явном виде отсутствует. Между тем, оно присутствует там в скрытом виде. Действительно, следует принять во внимание, что вывод о “качаниях” полюса был сделан на основе астрономических наблюдений, в основном по методу Талькотта [1,2] – которые проводились по ночам. Поэтому потоки данных с каждого пункта наблюдений, даже на интервалах времени в несколько ясных ночей подряд, не были непрерывными, а имели селекцию с периодичностью в солнечные сутки. Такая селекция лунно-суточной волны в (2) даёт не что иное, как синодическую волну с той же амплитудой – в этом убеждают значения лунно-суточной волны, взятые с 24-часовым дискретом во времени. Таким образом, произведение синодической и апогей-перигейной волн, порождающее волну с чандлеровским периодом, действительно налицо.
Следует отметить, что период апогей-перигейного цикла, вообще говоря, отличается от аномалистического месяца, который, по определению, равен интервалу времени между последовательными прохождениями Луны через перигей. Дело в том, что движение Луны вокруг Земли является сильно возмущённым, и, даже на одном её обороте, интервалы времени, во-первых, между перигеями, и, во-вторых, между апогеями, могут существенно различаться. Так, на рисунке приведены интервалы времени между последовательными апогеями и перигеями Луны, в солнечных сутках, на 2004-2005 гг., по данным [12].

Ясно, что о периоде апогей-перигейного цикла можно говорить лишь весьма условно, и что эффективная величина этого периода должна представлять собой некоторое среднее между изменяющимися длительностями “апогейного” и “перигейного” месяцев – с наиболее вероятным значением около 27.6 суток.
Уточним эту цифру. В таблице приведены периоды Т синусоид, у которых разности частот с синодической волной соответствуют значениям чандлеровского периода ТСН – из диапазона его изменяемости.
|
Т СН, сут |
410 |
415 |
420 |
425 |
430 |
435 |
|
Т , сут |
27.55 |
27.57 |
27.59 |
27.61 |
27.63 |
27.65 |
По данным А.Я.Орлова [13] и Международной службы вращения Земли (
IERS) [14], максимум спектра чандлеровских колебаний приходится на период » 428 суток – чему, по логике вышеизложенного, соответствует эффективный апогей-перигейный период в 27.62 суток.Теперь заметим, что в “лунных” колебаниях широты (2) имеется компонента, включающая произведение склонения Луны, которое изменяется с циклом, близким к сидерическому месяцу, на синодическую волну. Это произведение порождает не что иное, как годичную волну, амплитуда которой значительно превышает амплитуду годичной волны в (1), обусловленной годичным изменением склонения Солнца. Сумма этих двух годичных волн даёт, на наш взгляд, результирующую годичную компоненту изменяемости широт – происхождение которой, стало быть, оказывается никоим образом не связано с сезонными геофизическими процессами. Наконец, сумма годичной и чандлеровской волн даёт главную часть долгопериодической изменяемости широт, с известным характерным периодом биений: » 6.8 лет.
Амплитуда этой главной части, согласно (1) и (2), зависит от “истинной” широты места. Максимальные величины эквивалентных “смещений” полюса были оценены с помощью машинного моделирования, с учётом вышеупомянутой солнечно-суточной селекции данных. Мы получили, что максимальное годично-чандлеровское “смещение” полюса почти линейно убывает по мере увеличения “истинной” широты места. Так, при максимальной амплитуде склонения Луны (28о.5) и синфазности годичных компонент в (1) и (2), максимальное “смещение” полюса изменяется от примерно 7.3 м для широты 30о до примерно 4.8 м для широты 60о – соответствующий размах “качаний” полюса в два раза больше. Полученные цифры несколько не дотягивают до “рекордных” размахов, составлявших пару десятков метров. Но следует иметь в виду, что мы принимали в расчёт лишь годично-чандлеровское “смещение”, и не учитывали, в частности, весьма нерегулярный вклад, порождаемый произведением трёх синусоид в (2) – с тремя близкими периодами: апогей-перигейным, синодическим и сидерическим. Синфазная комбинация этого тройного произведения с годично-чандлеровским вкладом давала бы уже вполне удовлетворительные “рекордные” цифры. Добавим, что дополнительная нерегулярность должна привноситься изменениями апогей-перигейного цикла, вариациями амплитуды склонения Луны, и др. В результирующей картине оказывается весьма трудно выделить закономерности, помимо годичной и чандлеровской компонент.
Теперь кратко остановимся на весьма интересном вопросе о глобальных корреляциях у обсуждаемых неполярных изменений широт. Что касается долгопериодических вариаций широт, то их фазы в различных наземных пунктах скоррелированы таким образом, что концепция “качаний” полюсов как будто подтверждается. Иное дело – короткопериодические вариации. Так, фазы суточных вариаций широт на пунктах в северном и в южном полушариях скоррелированы, по логике вышеизложенного, таким образом, что концепция “качаний” полюсов приводила бы здесь к абсурду. А именно: пришлось бы сделать вывод либо о том, что ось вращения Земли не является прямой, а имеет то ли изгиб, то ли излом – либо о том, что Земля не покачивается вокруг прямой оси вращения, а испытывает невероятную вращающуюся волну деформаций, с растяжением и сжатием противоположных “боков”. По-видимому, сопоставление суточных вариаций широт на пунктах северного и южного полушарий заставило бы усомниться в справедливости концепции “качаний” полюсов – но ведь короткопериодические вариации широт, как отмечалось выше, попросту игнорировались.
Впрочем, даже и без этих сомнений, предпочтительнее выглядит вышеизложенная версия о неполярной природе изменяемости широт. Эта версия даёт предсказания, которые согласуются с опытными данными и по характерным периодам, и по амплитудам, и по фазовым соотношениям, а также весьма просто объясняет происхождение чандлеровской компоненты.
Иллюзия движения полюсов при современных методах наблюдений.
Вывод о “качаниях” полюсов был сделан на основе исключительно астрономических наблюдений, которые методологически и технически основаны на использовании местных отвесных линий. Но во второй половине ХХ в. астрономический вклад в отслеживание “качаний” полюса почти сошёл на нет.
В последнюю пару десятилетий IERS использует данные двух спутниковых методик – GPS-измерений и лазерной локации спутников – а также данные радиоинтерферометрии со сверхдлинными базами (РСДБ). Ни в одной из этих трёх методик не используются местные отвесные линии. Поэтому глобально скоррелированные уклонения этих линий не должны оказывать никакого влияния на работу этих трёх методик. Между тем, эти три методики, казалось бы, подтверждают вывод о периодическом движении полюса. Если это движение является иллюзией, то причина этой иллюзии должна быть здесь иной, чем при астрооптических наблюдениях.
Спутниковые методики.
Не может ли оказаться, что здесь годично-чандлеровские эффекты обусловлены недоучтёнными возмущениями спутниковых орбит?
Так, из-за вращения системы Земля-Луна, движение земной частотной воронки, порождающей земное тяготение и задающей околоземное, если можно так выразиться, “инерциальное пространство” [15], представляет собой вращательный “параллельный снос” [11]. Это должно приводить, на наш взгляд, к инерциальным эффектам при околоземном свободном движении пробных тел. Для расчёта соответствующих возмущений орбит ИСЗ можно применить выражения для эволюции параметров орбит при малых активных ускорениях ИСЗ [16]. В приближении нулевого эксцентриситета эволюционирует, главным образом, ориентация орбиты в пространстве – из-за действия составляющей aj активного ускорения ИСЗ, ортогональной плоскости орбиты. Для наклонения орбиты i и долготы её восходящего узла W имеем:
di/dt» (r/g M)1/2× cosJ × aj , (3)
dW /dt» (r/g M)1/2× sinJ × (sin i)-1× aj , (4)
где
r - радиус орбиты, g - гравитационная постоянная, M - масса Земли, J - полярный угол, характеризующий положение ИСЗ на орбите. Если ускорение aj мало изменяется за период обращения спутника t , то из уравнений (3) и (4) следует, что вектор нормали к плоскости орбиты совершает вращательные колебания с тем же периодом t и с амплитудным отклонением от среднего направления, равнымD a » (r/g M)1/2× aj /w , (5)
где w
=2p /t . При этом понятие “плоскость орбиты” утрачивает буквальный смысл, поскольку спутник отклоняется по своему курсу то “вправо”, то “влево” от расчётной траектории, пересекая её в четырёх точках. Максимальные угловые отклонения от расчётной траектории составляют при этом » D a /2.К каким последствиям должны приводить названные возмущения орбит при определении координат наземных пунктов с помощью
GPS? Шесть траекторий спутников GPS имеют одинаковые наклонения, около 55о, и равномерно разнесены по долготе. Луна делает оборот относительно орбит GPS за сидерический месяц, и примерно с этим же циклом изменяются амплитуды и фазы вращательных колебаний нормалей к орбитам. При этом спутники GPS сфазированно “колышатся” на орбитах – и, подобно тому, как генерируется вращающееся магнитное поле в устройствах трёхфазного тока, в рассматриваемом случае формируются вращающиеся векторы систематических ошибок определения координат наземных пунктов. Для оценки величины этих векторов, в качестве среднего амплитудного значения aj возьмём a× sin i и, с учётом собственного вращения Земли, для систематической ошибки определения широты наземного пункта (на умеренной широте) получим:D j » 0.5× (r/g M)1/2× (a× sin i/w )× sin(2p t/TSIN)× cos i. (6)
Поскольку ускорение
a имеет лунную апогей-перигейную вариацию (см. выше), произведение апогей-перигейной и синодической волн в (6) даёт чандлеровскую волну – с амплитудой эквивалентного линейного смещения около 6 м.Что касается “солнечного” вклада, то он должен представлять собой годичную волну с амплитудой, практически равной величине сдвига
d (см. выше), в направлении к Солнцу, системы орбит спутников относительно центра геоида [11], т.е. » 1.6 м.Тогда максимальный размах результирующей годично-чандлеровской волны должен составлять около 15 м. Причём, разности фаз этих волн для различных наземных пунктов таковы, что порождается иллюзия соответствующих “качаний” полюса.
РСДБ-методика.
Далёкие радиоисточники находятся за пределами сферы гравитационного действия Земли, и, казалось бы, связанная с ними опорная система координат – фактически, эквивалент системы “неподвижных звёзд” - свободна от пертурбаций на интервалах времени, характерных для рассматриваемой задачи. Это так, но РСДБ отнюдь не является независимым средством определения ориентации геоида по отношению к системе “неподвижных радиоисточников”. Дело в том, что в РСДБ-методике требуется синхронизация часов, находящихся на концах базовых линий, а эта синхронизация производится с помощью GPS. Вышеописанные годично-чандлеровские эффекты в движении спутников GPS должны трансформироваться в соответствующие систематические ошибки синхронизации часов на РСДБ-пунктах. Эти ошибки, в свою очередь, должны соответственно искажать разности моментов регистрации прихода импульсов на радиотелескопы – что в итоге должно порождать иллюзию годично-чандлеровских вариаций в ориентациях базовых линий. Таким образом, РСДБ-методика должна давать всё ту же иллюзию “качания” полюсов.
Небольшая иллюстрация.
Приведём кривую угловых “качаний” полюса в проекции на приполярный отрезок меридиана Гринвича, на более чем столетнем интервале, по данным IERS [14]. Первыми спутниками, наблюдения за которыми использовались для отслеживания “качаний” полюса, были спутники серии “Транзит”, запускавшиеся с апреля 1960 г. [1]. На кривой хорошо заметны результаты перехода на спутниковые методики.
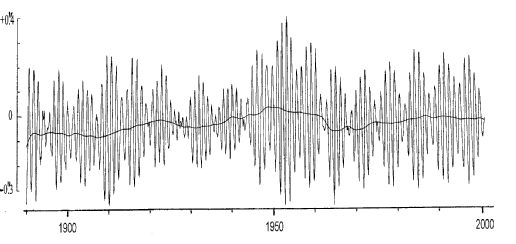
Невероятно, что после этой технической модернизации полюс стал “качаться” значительно упорядоченнее, поэтому комментарии обычно сводятся к тому, что спутниковые методики точнее астрономической и поэтому дают более истинную картину “качаний”. Но, на наш взгляд, дело здесь не столько в повышении точности, сколько в том, что, по сравнению с астрономическим методом, у спутниковых методик “чище” спектр возмущений, порождающих иллюзию движения полюса.
Заключение.
С учётом вышеизложенного, естественно объясняются корреляции, в широком диапазоне частот, между изменяемостью широт и вариациями силы тяжести. Но следствием нашего подхода является вывод об иллюзорности “покачиваний” Земли вокруг своей оси вращения.
Для физики далеко не безразлично – реальны эти “покачивания” Земли, или они иллюзорны. Первая из этих трактовок требует экзотических моделей строения Земли и сильных теоретических натяжек. Вторая же является естественным следствием подхода, основанного на представлениях об “унитарном” действии тяготения [15]. Очередным свидетельством в пользу справедливости этого подхода может служить полученная на его основе простая разгадка вековой тайны – о происхождении чандлеровской компоненты “качаний” полюса.
Автор благодарит В.И.Беленко за весьма полезное обсуждение.
Ссылки.
Источник:
http://newfiz.narod.ruПоступило на сайт: 29 октября 2005.