В данной статье мы постараемся ответить на вопрос: откуда берётся энергия, которая превращается в кинетическую энергию тела (малого, с массой m), свободно падающего по вертикали (на большое тело с массой M).

1) гравитационное поле, создаваемое телом M, совершает работу над телом m;

2) в кинетическую энергию тела m переходит энергия гравитационного взаимодействия тел M и m .

Оба эти ответа вызывают новые недоумённые вопросы. Если, во-первых, поле, создаваемое телом M, совершает работу, то энергия поля должна уменьшиться на величину совершённой работы. Но ведь это поле, а, значит, и его энергия, определяются только телом M, и, поскольку с телом M ничего не происходит, то и энергия его поля не должна уменьшаться. Иначе было бы возможно ослабить гравитационное поле планеты, многократно роняя один и тот же камешек. Далее, во-вторых: энергия гравитационного взаимодействия тел M и m, превращаясь в кинетическую энергию падающего тела m, также должна уменьшаться по мере уменьшения расстояния r между их центрами масс. С этим требуется согласовать тот факт, что тела M и m взаимодействуют, пока расстояние между ними не слишком велико - на бесконечном удалении они не взаимодействуют, т.е. при этом энергия их гравитационнного взаимодействия равна нулю. Математика легко и изящно делает требуемое согласование, приписывая энергии гравитационного взаимодействия отрицательный знак:

, (1)

где G - гравитационная постоянная. Но имеет ли физический смысл отрицательная энергия взаимодействия, которая превращается в положительную кинетическую энергию? Энергия, которая может быть отдана одним физическим объектом другому, положительна по своей сути, поэтому энергетический баланс принципиально отличается, например, от финансового баланса. Люди могут работать "в долг", но физические законы - нет.

Впрочем, об ошибочности обоих приведённых выше ответов можно судить по самому факту появления ОТО, ведь природа гравитации, якобы, вскрылась только благодаря этой теории. Согласно подходу ОТО, не требуется никаких превращений энергии для того, чтобы с ускорением двигать тело m: ускорение возникает единственно благодаря искривлению пространства-времени в окрестностях тела M. Эта красивая математическаи идея, на наш взгляд, лишена полноценного физического содержания. Ведь очевидно, что при свободном падении тела его кинетическая энергия растёт, поскольку именно кинетическая энергия, набранная им, может быть выделена, например, при его ударе о поверхность. Мы повторяем свой вопрос: какая же энергия превращается в кинетическую энергию свободно падающего тела? Или свободное падение, в рамках подхода ОТО, происходит с нарушением закона сохранения энергии?

На наш взгляд, закон сохранения энергии, конечно же, при свободном падении не нарушается. Проблемы с балансом энергий при свободном падении обусловлены неявным предрассудком о том, что энергия, которая станет кинетической энергией тела, должна быть сообщена этому телу откуда-то извне. Нам же представляется, что в кинетическую энергию свободно падающего тела превращатся энергия квантовых осцилляторов самого этого тела, т.е. его внутренняя энергия. Искривление пространства-времени в месте нахождения тела лишь направляет это энергопревращение и задаёт его интенсивность.

, (2)

где h - постоянная Планка, f - частота осциллятора. Из выражения (2) следует, что, при небольшом перемещении D r (таком, что D r<<r) в направлении к телу M, собственная энергия квантового осциллятора уменьшается на величину

. (3)

, (4)

где v - локальная скорость [1] (в нашем случае - вертикальная), то можно показать, что, в приближении v<<c, при падении квантового осциллятора с ускорением , уменьшение собственной энергии равно увеличению кинетической энергии . Выражение для энергетического баланса, описывающее свободное падение квантового осциллятора, имеет вид:

, (5)

и отличается от аналогичного выражения для случая свободного падения тела с массой m тем, что "масса" квантового осциллятора изменяется в процессе падения. Тем не менее, выражение (5) приводит к хорошо известному значению набираемой скорости при свободном падении:

, (6)

где - начальная скорость.

До сих пор мы неявно полагали, что квантовый осциллятор является элементарным, или свободным, т.е. он не входит в состав более сложно организованной структуры. Таким свободным осциллятором может являться, например, свободный электрон, испытывающий квантовые пульсации на частоте, соответствующей его массе покоя. У связанных же квантовых осцилляторов, т.е. входящих в состав какой-либо структуры, собственные энергии уменьшены на величину соответствующей энергии связи из-за "дефекта масс". Кроме того, как мы отмечали ранее [1,2], величины энергий связи подвержены кинематическим сдвигам, пропорциональным квадратам локальной скорости, что проявляется как квадратичный эффект Допплера. Выражение для энергетического баланса при свободном падении связанного квантового осциллятора имеет вид:

, (7)

где 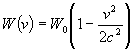- энергия связи, как функция локальной скорости. После приведения подобных и отбрасывания малых членов обнаруживается, что выражение (7) эквивалентно выражению (5). Это означает следующее: не смотря на то, что частоты связанных квантовых осцилляторов подвержены кинематическим сдвигам, а частоты свободных квантовых осцилляторов им не подвержены, все осцилляторы падают одинаково.

2. Grishaev A.A. Report for 1998 International Symposium on Acoustoelectronics, Frequency control and Signal generation. Russia, St.Petersburg - Valaam - Kizhi - St.Petersburg, 7-12 June 1998. Proceedings, p.33.

Источник: http://newfiz.i-connect.com